DTMF Application
DTMF Application Exercises
The keys on a standard telephone produce a sound when pressed, essentially composed of two main frequencies, forming a Dual-Tone Multi-Frequency (DTMF) signal.
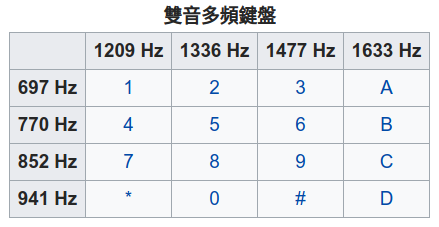
The DTMF keypad is a 4x4 matrix, with each row representing a high frequency and each column a low frequency, as shown below. When we press a key, a combination of a high and low frequency sine signal is transmitted. For example, pressing '1' generates two frequencies: 697 and 1209 Hz.
In this mini-unit, we'll use the Fast Fourier Transform learned previously to observe the frequencies of the keys and thereby decode the keypresses.
When Xiao Ming presses the telephone keys, Xiao Ying secretly records it with a sampling rate of 8000 Hz and amplitude adjusted to real numbers between -1 and 1. The recording, in wav format, is stored at this link. Try playing it to listen and download it to your computer.
Xiao Ying, having learned some basic FFT concepts, decides to decode it herself and writes the following piece of code in octave:
[y, fs] = audioread('dtmf-sample.wav'); % Load the audio file
plot(y);After execution, the following graph output can be observed.
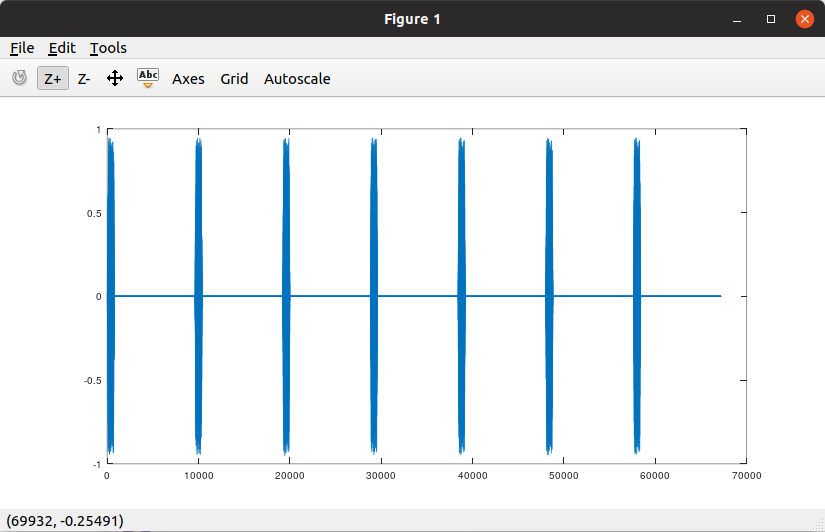
Please use help audioread to see how the audioread command is used and try Xiao Ying's code.
- Based on the graph above, Xiao Ying estimates that the phone number should have 7 digits. After careful observation, she finds that the signal for the first digit should have fewer than 1000 samples. If 1024 points are taken for FFT, the total duration of the frame is 1024/8000 seconds, so the frequency resolution , which is enough to distinguish the frequencies according to the DTMF standard. Xiao Ying decides to start from the 200th point, taking 1024 consecutive points to observe its spectrum. Thus, she writes another program as follows:
sample_rate = 8000; % Sampling rate
nstart = 200; % Start position of the frame
N = 1024; % Total number of points in the frame
[y, fs] = audioread('dtmf-sample.wav'); % Load the audio file
df = 8000/1024; % ΔF = 1/T < 8
ys = y(nstart:nstart+N-1); % Take the frame
ysf = fft(ys); % Calculate FFT of the frame
fnum = (-N/2:(N/2)-1)*df; % Calculate the corresponding frequency points
plot(fnum, abs(fftshift(ysf))); % Plot the spectrumThe execution result is as follows:
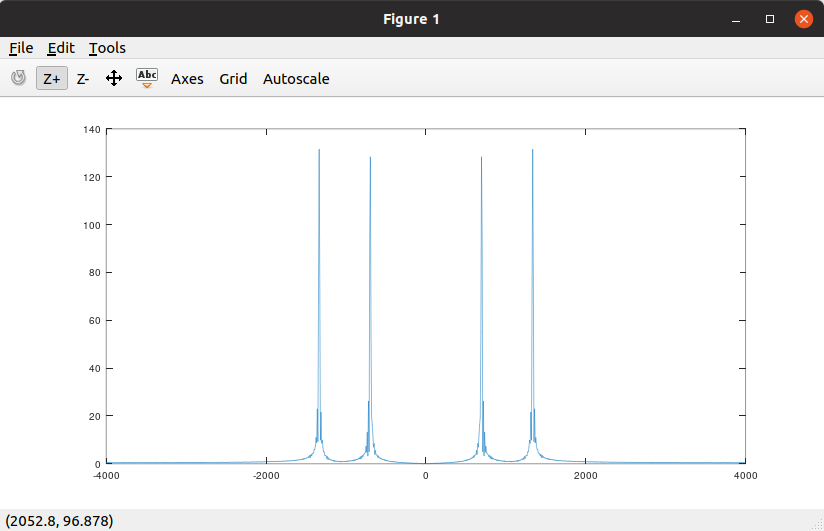
- Xiao Ying then carefully checks the two peaks of the signal using the graph's zoom function and finally deduces they are likely 697 and 1336 Hz. From this, Xiao Ying confirms that the first digit of the phone number should be 2. Try to follow the above program and practice using the graph zoom function to check if Xiao Ying's judgment is correct.
Exercise 5
