快速傅立葉轉換

Jia-Yin2024年3月7日大约 5 分鐘

離散傅立葉轉換 (Discrete Fourier Transform, DFT)

前面提到， $s(t)$ 的傅立葉轉換為

S(f) = \int_{-\infty}^{\infty} s(t) e^{-j 2 \pi f t} \, dt

在許多應用當中，我們很難找到 $s(t)$ 的函數形式，即便能夠找到，在計算積分的時候，也很可能找不到封閉的積分形式，因此大多數的情況之下，我們會使用數值的方式來計算傅立葉轉換，最常見的計算方法，可能是離散傅立葉轉換 (Discrete Fourier Transform, DFT)。

假設信號 $s(t)$ 在一個區間取樣 $N$ 個點，其值為 $s_0, s_1, \cdots, s_{N-1}$ ，定義其 DFT 為：

S_k = \sum_{n=0}^{N-1} s_n e^{-j\frac{2\pi}{N}nk}

注意在上式中，當 $k$ 增加 $N$ 時，其值不變，因此主要的轉換值為 $S_0, S_1, \cdots, S_{N-1}$ 。

比較上述的積分式以及 DFT 的定義，會發現兩個公式有一些相似的地方，由於 DFT 處理的是取樣之後的信號值，而且是只侷限在一個區間的 $N$ 個點，因此我們可以把 DFT 算出來的 $S_k$ 值當作是 $S(f)$ 的近似取樣值。

根據前面的取樣定理，假設取樣速度為 $f_s$ ，則可以還原的信號頻率介於 [- $f_s/2$ , $f_s/2$ ] 之間，將此頻率範圍均勻分成 $N$ 個等分，每等分大小為

\Delta f = \frac{f_s/2 - (-f_s/2)}{N} = \frac{f_s}{N} = \frac1{NT}

這邊 $T$ 為取樣時間間隔，因此 $NT$ 為整個取樣區間的總共時間。歸納以上提到的 DFT 的幾個重要性質如下：

將 $N$ 個時間取樣點 $s_0, s_1, \cdots, s_{N-1}$ ，轉換為 $N$ 個頻率取樣點 $S_0, S_1, \cdots, S_{N-1}$ ，其中 $S_k$ 是週期性的，週期為 $N$ 。
假設取樣速度為 $f_s$ ，則可以決定的最高頻率值為 $f_s/2$ 。
取樣頻率之間的間隔為取樣總時間長度的倒數。

DFT 還有很多其他重要的性質，這邊再列出三個重要性質：

DFT 運算是線性的，亦即 DFT( $ax+by$ ) = $a$ DFT( $x$ ) + $b$ DFT( $y$ )。
如果 $s_n$ 是實數，則 $S_k = S^*_{-k} = S^*_{N-k}$ ，此處 * 表示共軛複數。
根據上述的 DFT 公式，可以得到 DFT 的反轉換如下：

s_n = \sum_{k=0}^{N-1} S_k e^{j\frac{2\pi}{N}nk}

快速傅立葉轉換 (Fast Fourier Transform, FFT)

在計算離散傅立葉轉換的時候，可以利用公式中許多對稱和共軛的性質來加快計算過程，這種快速計算的方法稱為快速傅立葉轉換，簡稱 FFT。FFT 有不同的計算形式，但實際上就是快速計算 DFT 的算法。FFT 的逆轉換稱為 Inverse FFT，或稱為 IFFT。

一般在信號處理時，我們多使用快速傅立葉轉換 (FFT) 來計算其頻譜，使用快速傅立葉轉換時，應牢記以下幾個重點：

假設用來分析的信號段有 $N$ 個點，且其取樣間隔為 $T$ ，則此信號段總長為 $NT$ ，且取樣速度為 $f_s=1/T$ 。
根據取樣定理，可以觀察的頻率範圍為 $[-f_M,f_M]$ ， $f_M=f_s/2$ 。
$N$ 個時域點做 FFT 之後變成 $N$ 個頻域點，故頻率解析度，亦即相鄰頻率點的間隔為 $2f_M/N = f_s/N = 1/(NT)$ 。簡單說，取樣時間總長的倒數就是頻率取樣點之間的距離，也就是頻率解析度。
要記得取樣速度的一半，是可觀察的最大頻率；取樣總長的倒數是頻率解析度。
如果是實函數的話，做完 FFT 之後，其正頻率和負頻率相對的值會是共軛複數。

我們現在來觀察帽子函數的頻譜，帽子函數 rect(t) 圖形如下：

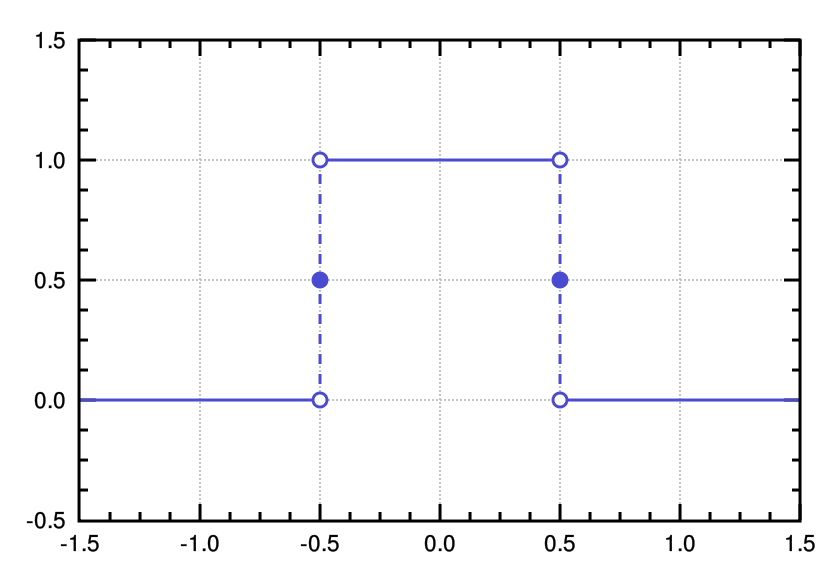
使用 MATLAB/Octave 觀察其頻譜步驟如下：

假設取樣範圍從-1.5到1.5，每隔0.1取一點，先計算時域信號：

t1 = -1.5:0.1:-0.6;
t2 = -0.4:0.1:0.4;
t3 =  0.6:0.1:1.5;
t = [t1 -0.5 t2 0.5 t3];
s = [zeros(size(t1)) 0.5 ones(size(t2)) 0.5 zeros(size(t3))];
plot(t, s);

這個程式片段寫得有點繁瑣，不過很容易理解，執行看看結果是否正確。

計算頻譜，直接使用 fft 函數將上面的時域信號轉到頻域，應注意轉出來的結果為複數，我們先觀察其振幅。

sf = fft(s);
plot(abs(sf));

注意在上面的程式中，畫圖時只給了y軸，橫軸會是點數，得到的結果如下：

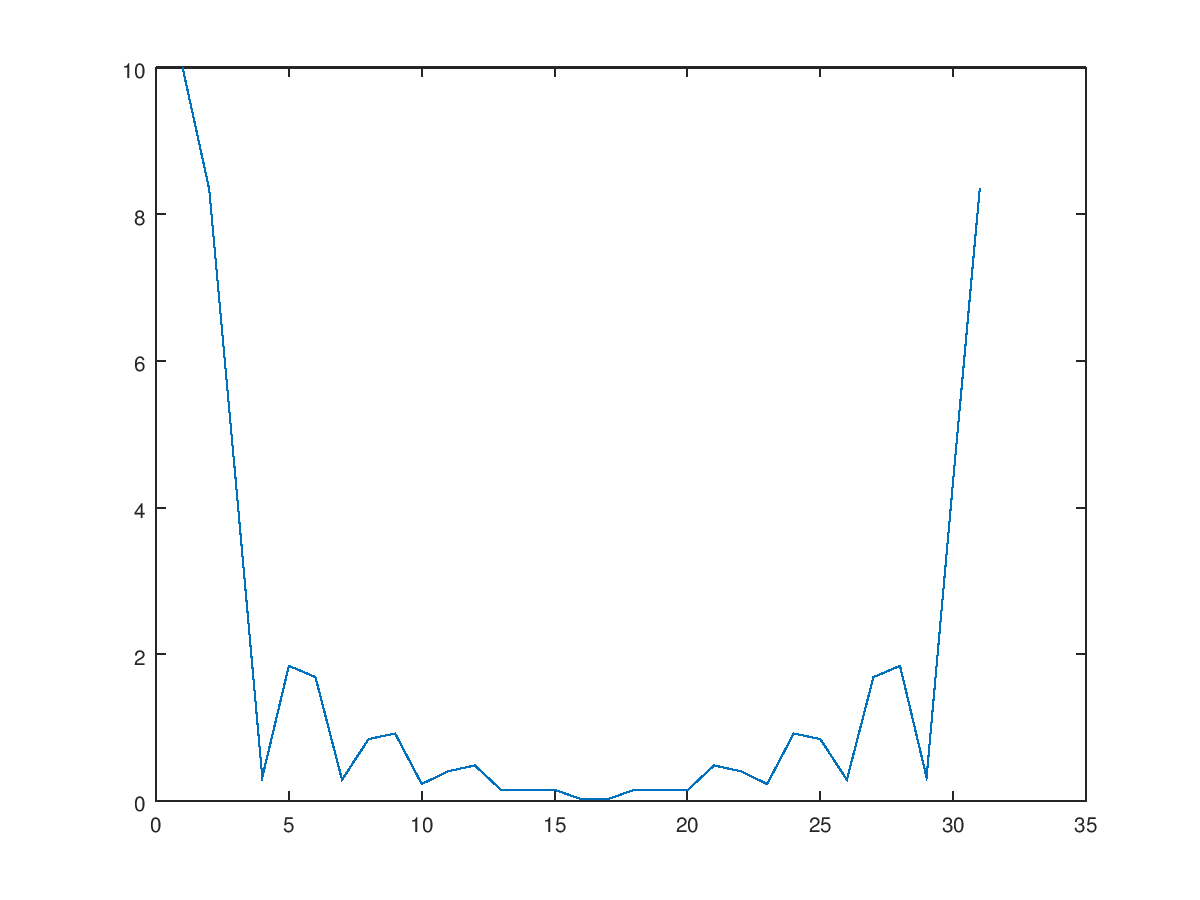
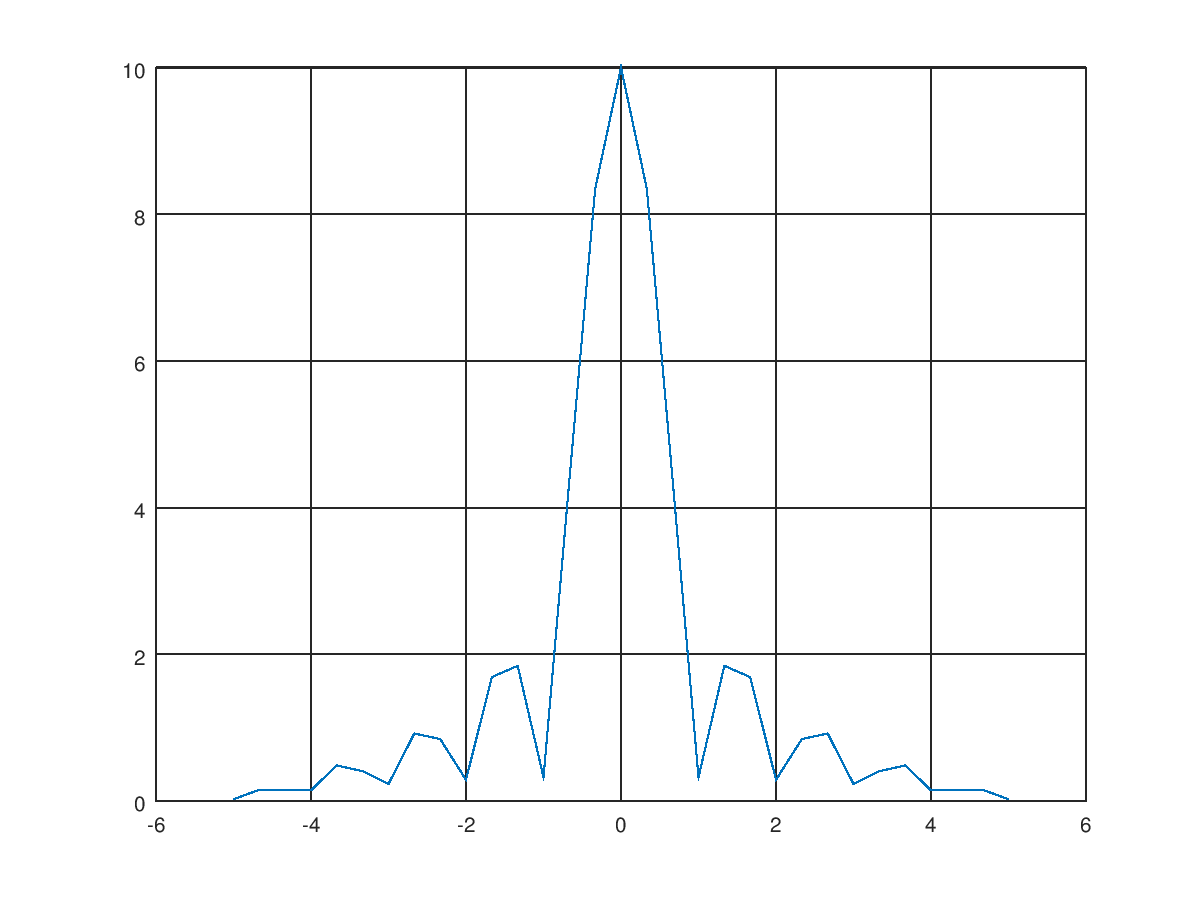
上面提過實函數的 FFT，其正頻率和負頻率相對的值是共軛複數。實際上我們現在看到的圖形中，圖的右半邊應該移到負的那邊去才對。MATLAB 里面有一個 fftshift 就做這事。另外，最大頻率為取樣率一半=5，間隔為總長倒數=1/3，我們要把橫軸 (頻率) 加上去。

sf = fft(s);
sf = abs(fftshift(sf));
f = -5:1/3:5;
plot(f, sf);
grid on;

最後得到修正的圖如下，這個圖形就是 sinc 函數的振幅。

完整程式碼如下：

t1 = -1.5:0.1:-0.6;
t2 = -0.4:0.1:0.4;
t3 =  0.6:0.1:1.5;
t = [t1 -0.5 t2 0.5 t3];
s = [zeros(size(t1)) 0.5 ones(size(t2)) 0.5 zeros(size(t3))];
sf = fft(s);
sf = abs(fftshift(sf));
f = -5:1/3:5;
plot(f, sf);
grid on;

練習 4

上面的頻譜圖看起來並不是非常平滑，請修改程式的參數，讓畫出來的頻譜變得更加平滑。