我們假設要處理的信號為實函數 s(t),其頻譜為 S(f),而且假設 S(f) 具有的最大頻率成分不超過 fM,注意實函數的頻譜基本上是對稱 y 軸的,如下圖所示:
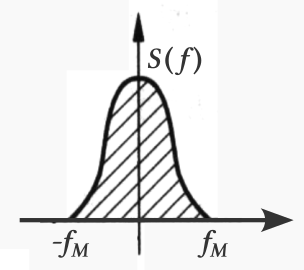 s(t) 的頻譜 S(f)
s(t) 的頻譜 S(f)前面提過,從類比信號到數位信號,基本上要先經過取樣以及量化的過程,其中量化是不可逆的,會引進所謂的量化雜訊。
現在來談取樣的部分。
假設信號為 s(t),每隔時間 T 取樣一次,取樣的結果為 sn=s(nT)。在數學上,我們可以假想,取樣的方式等同於用梳子函數乘上原來的信號 s(t),也就是 ШT(t)s(t),如下圖所示:
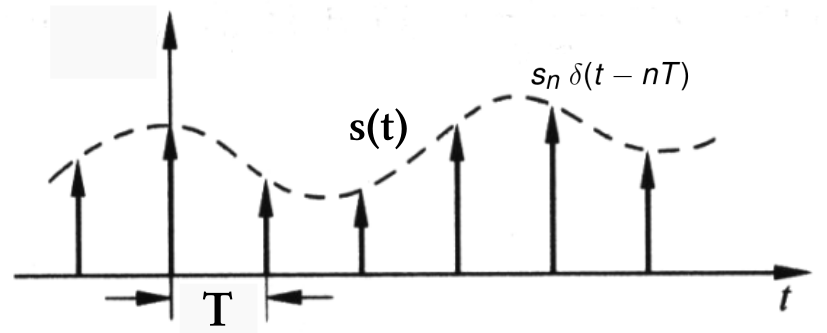 對 s(t) 函數取樣
對 s(t) 函數取樣這邊我們不用去管 δ 函數會趨近於 ∞ 的問題,只要管 δ 函數前的係數就好了。
信號取樣之後,來看一下它的傅立葉轉換,也就是取樣後的頻譜。依據前面所述的內容:
F{ШT(t)s(t)}=F{ШT(t)}∗F{s(t)}=T1ШT1(f)∗S(f)
由於 Ш1/T(f) 函數由一堆 δ 函數構成,而 δ 函數與任一函數做摺積時,仍為該函數,但中心則平移到 δ 函數的中心點,亦即
ШT1(f)∗S(f)=n=−∞∑∞δ(f−n/T)∗S(f)=n=−∞∑∞S(f−n/T)
也就是取樣後的頻譜如下(先不考慮振幅):
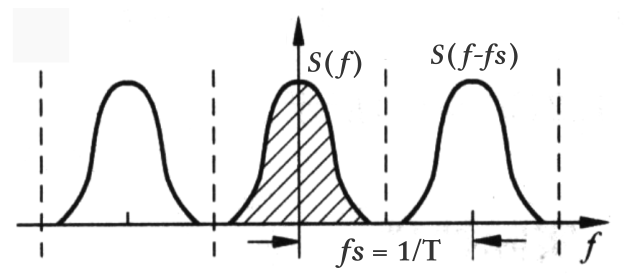 s(t) 取樣後的頻譜
s(t) 取樣後的頻譜注意,上圖假設 fs>2fM,因此重覆的頻譜之間並沒有任何重疊。如果 fs<2fM,則重覆的頻譜彼此之間就會交疊在一起。
如果 fs>2fM,則重覆的頻譜之間不會有任何重疊,那麼我們只要取中間斜線部份的那塊頻譜,當作我們要還原的信號,這樣一來,由於信號的頻譜完全相同,那麼信號也就完全相同,換句話說,理論上可以透過取樣的結果將原來的信號還原回來。取樣率 fs=2fM 被稱為奈奎斯特取樣率,相應的頻率 fM 被稱為奈奎斯特頻率。
還原的方法,以頻域上來說,就是將取樣後的頻譜乘上一個帽子函數,等於將信號做低通濾波,也就是只保留中間斜線的頻譜區域,並將其他區域的頻率過濾掉。以數學式來看,可以表示為(這邊先不考慮振幅):
(n=−∞∑∞S(f−n/T)) Π(f/fs)=S(f)
另外也可以從時域來看,將上式做逆傅立葉轉換,可以得到時域信號。由於頻域相乘,時域會變成摺積,另外帽子函數的反轉換為 sinc 函數,因此時域信號可以表示為(先不考慮振幅):
s^(t)=(ШT(t)s(t))∗sinc(fst)=(n=−∞∑∞snδ(t−nT))∗sinc(fst)=n=−∞∑∞sn sinc(fs(t−nT))=n=−∞∑∞sn sinc((t−nT)/T)
此結果如下圖所示,等於是在每個取樣點上,放置一個縮放過的 sinc 函數,這個 sinc 函數在取樣位置的值為 1,在其他取樣位置的值為 0。因為這樣的緣故,有時候也稱 sinc 函數為取樣函數。
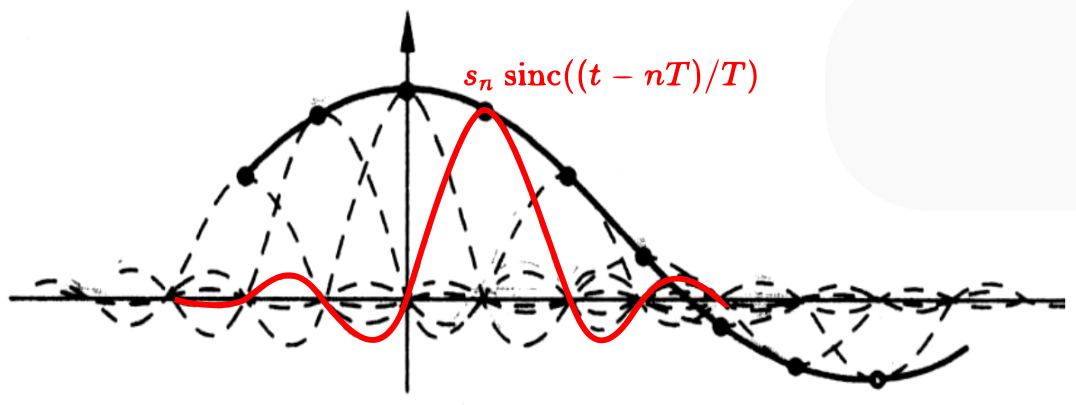 信號還原的時域等效圖
信號還原的時域等效圖- 上述的內容,假設信號的頻寬是有限的,請問這樣的假設在現實的物理世界中,是合理的假設嗎?請提出你的看法和理由。
- 上述的推論過程中,假設取樣速度高過信號最高頻率的 2 倍。如果實際上取樣速度不到信號最高頻率的 2 倍,會發生什麼結果?




