幾個常用函數

rect 函數

定義 rect(t) 函數如下：

$$\text{rect}(t) = \begin{cases} 1, & \text{if } |t| < \frac{1}{2} \\ \frac{1}{2}, & \text{if } |t| = \frac{1}{2} \quad (\text{optional condition}) \\ 0, & \text{if } |t| > \frac{1}{2} \end{cases}$$

其圖形如下圖所示，由於形狀像帽子，我們有時也將其稱為帽子函數 $\Pi(t)$：

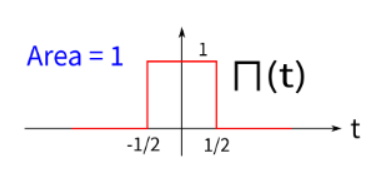rect(t)

sinc 函數

定義 sinc(t) 函數如下：

$$\text{sinc}(t) = \begin{cases} \frac{\sin(\pi t)}{\pi t}, & \text{if } t \neq 0 \\ 1, & \text{if } t = 0 \end{cases}$$

其圖形如下圖所示：

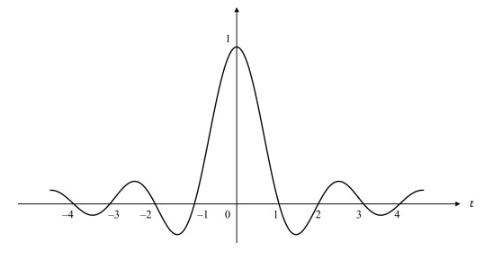sinc(t)

注意： $\mathcal{F}\{\Pi(t)\} = \text{sinc}(f)$， $\mathcal{F}\{\text{sinc}(t)\} = \Pi(f)$， 兩者互為傅立葉轉換對的關係。

$\delta$ 函數

定義 $\delta(t)$ 函數為

$$\delta(t) = \lim_{\epsilon \to 0}\ \frac{1}{2\epsilon}\ \text{rect}\left(\frac{t}{2\epsilon}\right)$$

這裡 $\text{rect}(t)$ 是矩形函數，當 $-\frac{1}{2} \leq t \leq \frac{1}{2}$ 時為 1，其他情況為 0，也可以記為 $\Pi(t)$。當 $\epsilon$ 趨近於 0 時，矩形函數的寬度也趨近於0，高度則趨近於 $\infty$，但仍保持其積分值為 1，如下圖所示：

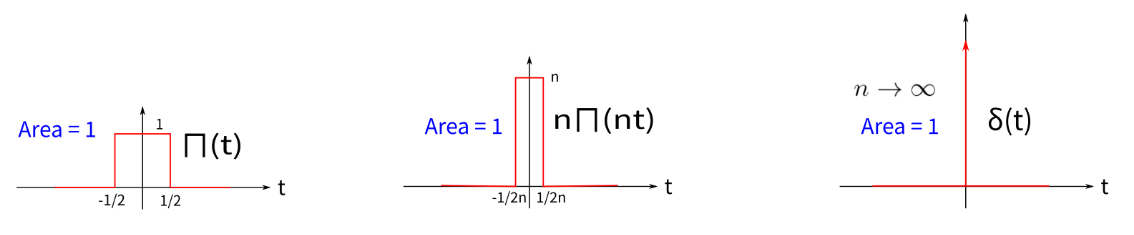$\delta(t)$ 函數的一種表達方式

$\delta(t)$ 有許多重要的特性與應用，以下是本單元會用到的幾個：

$$\mathcal{F}\{\delta(t)\} = 1$$

$$\mathcal{F}\{1\} = \delta(f)$$

$$\mathcal{F}\{e^{j2\pi f_0t} \} = \delta(f-f_0)$$

$$\begin{align*} f(t) * \delta(t-t_0) &= \int_{-\infty}^{\infty} f(t-\tau) \delta(\tau - t_0) \, d\tau \\ &= f(t-t_0) \end{align*}$$

comb 函數 (梳子函數)

定義 comb 函數如下：

$$\text{comb}_T(t) = \sum_{n=-\infty}^{\infty} \delta(t - nT)$$

或者將其簡寫為 $\text{Ш}_T(t)$，圖形如下：


$\text{Ш}_T(t)$ 為週期性函數，可以求出其傅立葉級數 $c_n=1/T$，故

$$\text{Ш}_T(t) = \sum_{n=-\infty}^{\infty} \frac1T\ e^{j 2 \pi nt/T}$$

進一步可以得到：

$$\begin{align*} \mathcal{F}\{\text{Ш}_T(t)\} &= \frac{1}{T} \sum_{n=-\infty}^{\infty} \delta(f-n/T) \\ &= \frac{1}{T}\ \text{Ш}_{\frac{1}{T}}(f) \end{align*}$$

故梳子函數的傅立葉轉換仍為梳子函數，但 $\delta$ 函數之間的寬度在時域和頻域成反比，高度也會有所變化，如下圖所示：

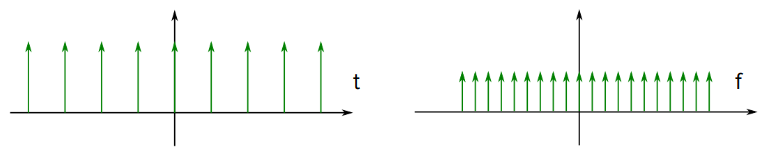$\text{Ш}_T(t)$ 的傅立葉轉換

練習 2

本頁的說明內容，許多地方並沒有詳細推導其中的過程。請使用生成式 AI 找出推導過程，並仔細檢查以確認其推導無誤。可以將過程複製下來，或者直接分享生成式 AI 的互動連結。